Okay, first off, this was supposed to be up a good while ago, but a combination of real life and work got in the way far more effectively than I had planned. Anyway, today’s diminishing returns formula is roots.
More generally speaking, we’re looking at x ^ y where y is some power that
diminishes your end result. There are really two general formulae that emerge
from this, and they’re very different, but both worth exploration:
0 < y < 1: The square root of X can be denoted asx ^ (1/2); cube-root,x ^ (1/3); etc. When speaking of roots, this is of course the range of y that people mean.y < 0: This is really not related to roots other than sharing the very broad definition ofx ^ y where y < 1. However, it’s worth exploring briefly because (a) it produces interesting diminishing returns for a set limit (x ^ -1, for instance, is the same as1 / x), and (b) even though the broad definition fits this and roots, they do dramatically different things. It’s good to see how generalizing a formula can sometimes lead to a dramatically different situation.
The two forms can both be useful, but in very different situations.
Roots
Square (or cube or quad or…) root formulae can be pretty basic, and have been used in real games I’m almost entirely certain I may have possibly played once (the names of which escape me, sadly). The first time you want a reward, you must get 1 kill. Next reward at 4, next at 9, then 16, etc. Easy pattern to follow, no upper limit, and while diminishment is fairly fast, it’s still more generally useful than a logarithmic formula, and far easier to modify for a specific situation.
In fact, according to this
article, written by (the?
a?) developer of the Lost Souls MUD, square roots (again, x ^ 0.5) are the
basis in what the author believes is the best general-use diminishing returns
formula:
factor = input_value / scale_number
position = (sqrt(8 * factor + 1) - 1) / 2
output = position * scale_number
Line 1 is used to deal with input translation so the numbers are on a nice scale. Line 2 is your basic diminishing returns formula, modified to produce triangular numbers (1,3,6,10,15,…). Line 3 converts the output to be on the same scale as the input.
The system slightly modifies input and output, and even does some interesting translation in the formula itself. But the curve is what we care most about, and in this case it’s a square-root formula, so it will produce some form of a square-root curve.
Note: This is a great example of how to customize a “base” formula. You could be customizing for readability, easier management of numbers, or just producing a slightly different texture.
An important note here is that just changing the exponent will significantly
modify the behavior of the curve you’re working with. Take a look at the
graphs below. Red is x^(1/10), Green is x^(1/2), Blue is x^(3/4), and
yellow is x^(9/10).
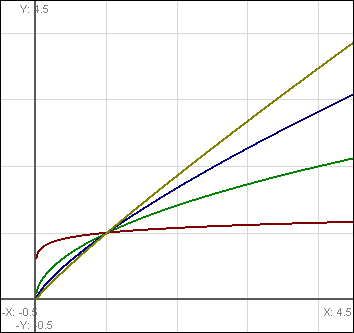
Note in particular that the Red graph has a very strong breaking point, before which it increases faster than the other graphs, but after which it diminishes incredibly fast. The others aren’t like this, even when zoomed out:
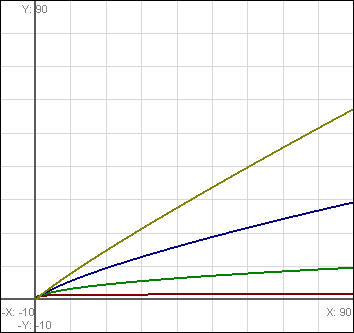
This is very different than logarithms. With logarithms, every single graph, no matter the base, will eventually have a very strong breaking point, which makes it tricky to modify the curve to be used outside of very specific situations. With roots, it’s a lot easier to just change the exponent to get a curve that fits any situation.
Negative Exponents
Negative exponents are a limit-based formula, and decrease output instead of
increasing it as you put more in. But they still diminish the amount of
change to output, and can easily be translated to work either way: 1 - ((x +
1)^-1), for instance, will create a formula that gives zero when x is 0, and
slowly moves closer and closer to 1, but never reaches it.
These are drastically different than roots, and it’s important to realize that
in the general formula of x ^ y, once you switch to a negative number for
y, you’re no longer looking at anything remotely like roots.
There aren’t any real-world examples that I personally have seen for this kind
of formula, and while I find it to be a fun one for building a system that
maxes out at a set value, the diminishment rate is rather crazy if not handled
carefully. The vanilla formula, x^-1, has the following set for outputs
when the input is in the range of 1-10: [1, 0.5, 0.3333, 0.25, 0.2, 0.1666,
0.1429, 0.125, 0.111, 0.1]. Note that the first drop gets you 50% of the way
to 0, the biggest drop by a huge factor.
There are clever ways to “fix” this, such as 1/sqrt(x) or grabbing a
different part of the curve, such as 1 - (1000 / (1000 + x)), and if you
truly need a limit-based system it may be worth figuring out, but it’s
probably worth looking at either exponential decay or a convergent series
rather than this.
Next time, I’ll dive deeper into both of those systems. Enjoy!
(All images were produced via GraphCalc)
Diminishing returns articles on Nerdbucket:
3 Replies to “Diminishing Returns in Game Design: Roots and Negative Exponents”