Finally, another exciting episode of NAME… THAT… DIMINISHING RETURNS FORMULA!!! Today we look at exponential decay and the convergent series, both of which are in my mind the only limit-based formula that should be considered for 99% of situations.
Why, then, did I bring up negative exponents in the last article? Mainly because it made sense to group that little tidbit with roots since the general formula is the same. Plus, roots work nicely in diminishing returns formulae, so it’s quite possible readers would latch on to that and ignore the little blurb about negative exponents altogether. That’s my hope, anyway.
Convergent Series
Look it up in Wikipedia, folks: the convergent series explained in plain English. Well, semi-plain. Anyway, their list of examples should clue you in. Note that not all convergent series apply to diminishing returns formulae – the example of alternating signs on the reciprocals of positive odd numbers would be lousy, because each extra amount of input added to the system isn’t necessarily increasing output. In fact, if you used that formula as-is, you’d notice quickly that your user is better off stopping after a single input (at the 1/1) if they’re going for a large number, or stopping at the second input (-1/3) if they’re going for a smaller number.
No, we’re always looking for a formula that rewards every bit of input, even if that reward is trivial and nearly meaningless. We never punish somebody for putting more into the system. Or if we do, we no longer call it “diminishing returns”.
So I’m actually only looking at the simplest case here – you start at some hard-coded base for the first input-to-output function, choose a decay rate, and just multiply again and again to get the next level of output:
f(0) = 0
f(1) = Base
f(x) = f(x - 1) * Decay
You’re only computing the next step’s output in the above formula, not the total output. Essentially the final output is a giant sum formula, taking the entire series and adding it all up. And note that this is a generalized form of the reciprocals of 2. If Base is set to 1 and Decay is set to 0.5, you get that exact series.
While it’s fairly easy to customize this formula by mucking with Decay, that’s about all I like about this formula (which, interestingly, still makes me prefer it to negative exponents). It can be very slow to compute if you want a large range of numbers (try summing the first million reciprocals of two), and it doesn’t have the infinite precision of a traditional formula. Those two pieces combined make it less than ideal unless you have a relatively small set of numbers you want to work with. It is a limit-based formula, and it’s rather easy to determine the limit – take the reciprocal of Decay, but having to support a small range of numbers makes this quality a lot less useful.
Anyway, there it is.
Exponential Decay
Exponential decay is by far my favorite limit-based formula for diminishing returns. It’s pretty easy to tweak, always moves from 1 down to 0 (so it’s easy to scale via negation and multiplication), and even the plainest version of the formula has usefulness.
For my purposes I’m usually looking for a formula that moves from 0 to some maximum, so the first thing I do to this formula is invert it and multiply it:
f(x) = Max * (1 - e^(-Cx))
Much like roots, we can tweak a single variable, C, to greatly differentiate the output. The following graph shows five formulae, all a form of 10 * (1 - e ^ (-Cx)):
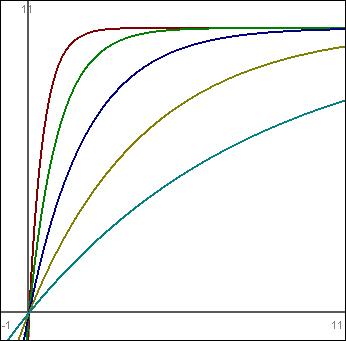
From left to right:
- Red: C = 2
- Green: C = 1
- Blue: C = 0.5
- Yellow: C = 0.25
- Cyan: C = 0.125
If you zoom out far enough and examine the graphs, you’ll notice that they all actually look the same, which is potentially problematic – much like logarithms, you could run into a situation where you can’t tweak C enough to get things the way you want them in order to have a graph that works for every possible range of input that any game could have…. Here’s that last graph, but in a view that allows you to see an x range of -1 to 200:
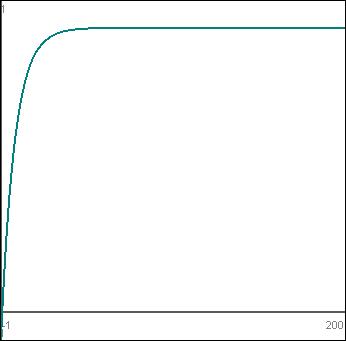
Well now, it suddenly looks an awful lot like the previous red graph, doesn’t it? What gives?!?
It’s important to note that when dealing with a limit-based formula, this is life. The formula must constantly increase output while still having a set, never-to-be-hit-but-always-moving-nearer limit. By nature, it will not be “just right” for all ranges, and will indeed have to be tweaked for every situation.
The main appeal here is that it still has a less significant breaking point than negative exponents, is far less CPU-intensive than building a custom convergent series, and is very easy to tweak. To get that “sweet spot” on a negative exponent or logarithmic graph, it can be a painstaking process. Same with building out just that perfect convergent series. But to get a workable exponential decay graph just requires modifying Max and C as necessary. There will inevitably be a strong-ish breaking point somewhere, but it’s very little effort to tweak the graph to work well for a specific situation.
Next time (hopefully soon-ish maybe…?), I’ll write a summary! A SUMMARY! OH WHAT JOY!
Diminishing returns articles on Nerdbucket:
2 Replies to “Diminishing Returns in Game Design: Exponential Decay and Convergent Series”